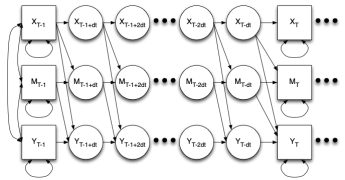
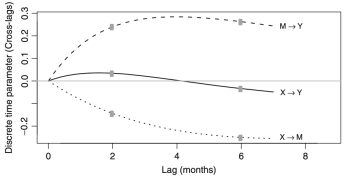
Time is unlike any other variable. This chapter considers the difference in perspectives offered by discrete-time and continuous-time approached to mediation. The differences in how one conceptualizes time have the potential to alter core mediation concepts as direct and indirect effect, complete and partial mediation, and even what constitutes a “mediation” model.
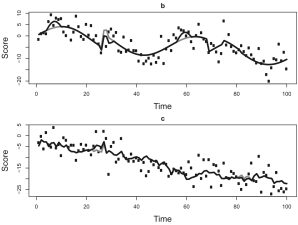
This essay reviews emerging trends in modeling repeated measures data. Three longitudinal models are discussed: panel model designs, growth curve models, and intensive within-person assessments. Continuous time models for panel data are discussed. The analysis of intensive within-individual observations is also considered, including work that limits the generalizability of interindividual studies to individual outcomes.
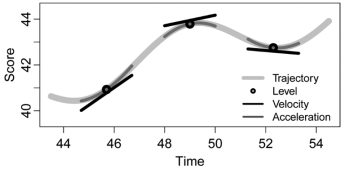
A wide variety of models can be understood in terms of the level, velocity, and acceleration of constructs: the zeroth, first, and second derivatives, respectively. Conceptualizing change in terms of derivatives allows precise translation of theory into method and highlights commonly overlooked models of change. We introduce the language of derivatives.
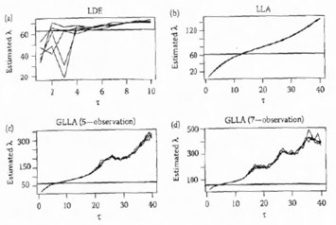
Using embedded and observed data matrices, a statistical approach to differential equation modeling is presented. This approach appears robust to short, poorly sampled time series with large proportions of measurement and dynamic error, as is common in psychological research.
Intraindividual measures, such as intraindividual standard deviation or coefficient of variation, are incomplete representations variability. Studying variability can be made more productive by examining specific time scales. Furthermore, examination of variance in observed scores may not be sufficient. A method is introduced that uses estimated derivatives to examine variability at multiple time scales.
This article considers the estimation of damped linear oscillators with psychological data. The formulas of the new method presented in this chapter, which related the τ-conditional and τ-corrected estimates of model parameters, are described.
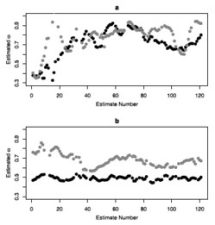
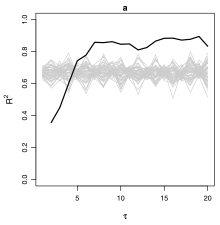
Methods for fitting the damped linear oscillator model using differential equation modeling can yield biased parameter estimates when applied to univariate time series. The bias depends on a researcher-selected, smoothing-like parameter. This article explores a technique that uses surrogate data analysis to select such a parameter, thereby producing approximately unbiased parameter estimates.