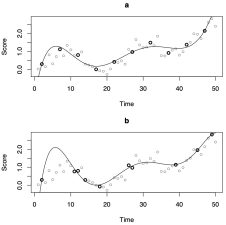
Effective interventions may not be limited to changing means, but instead may also include changes to how variables affect each other over time. Continuous time models offer the opportunity to specify differing underlying processes. A substantive example compares models that imply different underlying continuous time processes using panel data.
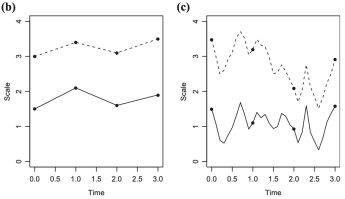
Time is unlike any other variable. This chapter considers the difference in perspectives offered by discrete-time and continuous-time approached to mediation. The differences in how one conceptualizes time have the potential to alter core mediation concepts as direct and indirect effect, complete and partial mediation, and even what constitutes a “mediation” model.
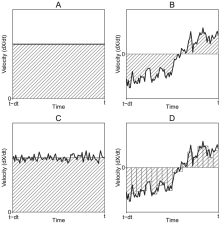
Stochastic differential equation (SDE) models are a promising method for modeling intraindividual change and variability. This method uses structural equation modeling (SEM) conventions to simplify SDE specification, the flexibility of SEM to expand the range of SDEs that can be fit, and SEM diagram conventions to facilitate the teaching of SDE concepts.
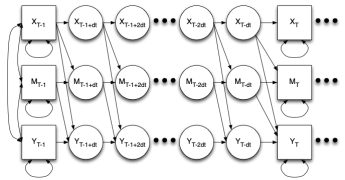
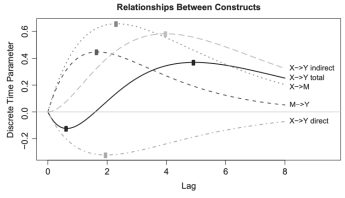
Mediation models based on cross-sectional data can produce unexpected estimates, so much so that making longitudinal or causal inferences is inadvisable. Even longitudinal mediation models produce estimates are specific to the lag between observations, leading to debate over lag selection. Using continuous time models, one can estimate lag-independent parameters.
Historically, it has been easier to describe differences between groups of people, rather than describe the dynamic ways that people change. This chapter introduces dynamical systems and of continuous time models. Two methods are introduced for the fitting of continuous time models to observed data: the approximate discrete model and latent differential equations.