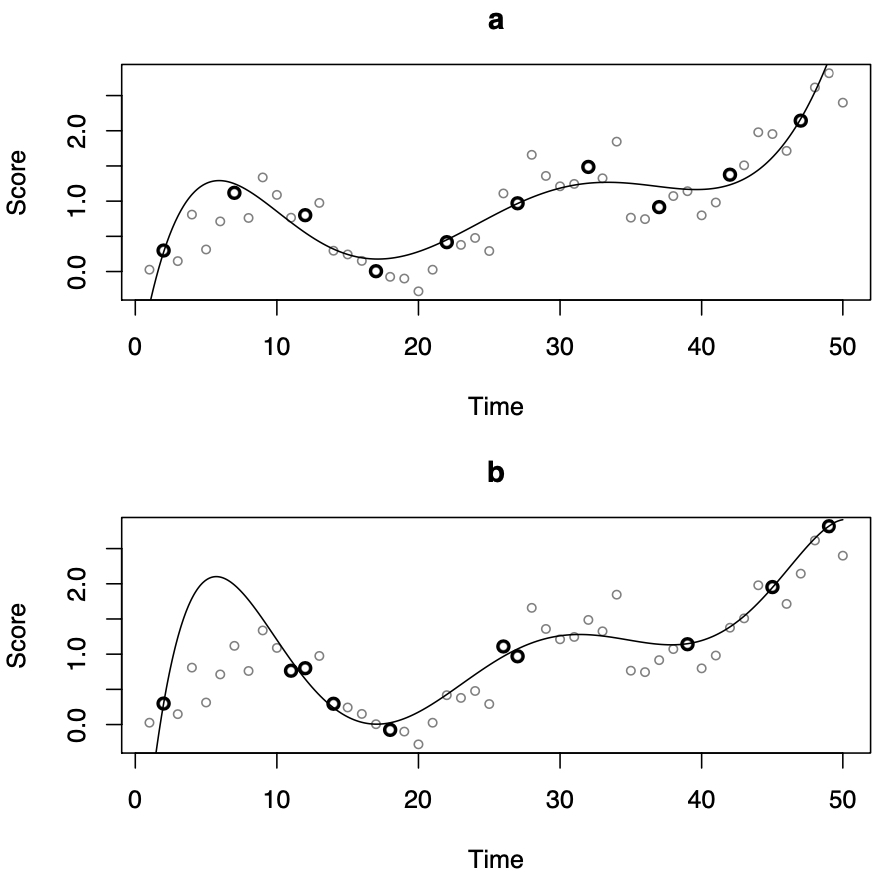
Historically, it has been easier to describe differences between groups of people, rather than describe the dynamic ways that people change. This chapter introduces dynamical systems and of continuous time models. Two methods are introduced for the fitting of continuous time models to observed data: the approximate discrete model and latent differential equations.
Abstract
Historically it has been easier to focus on measuring and describing differences between groups of people rather try to describe the dynamic ways that people change. Dynamical systems are mathematical models that aim to describe how constructs change over time. Frequently these models are continuous time models; models that try to capture the function that underlies a set of observations. This chapter introduces the concept of a dynamical system and of continuous time models. Two methods are introduced for the fitting of continuous time models to observed data: one using the approximate discrete model for a first-order autoregressive model and the second using a method of estimating latent derivatives for a second-order autoregressive model.
Code and Other Content
Code here
Citation
Deboeck, P. R. (2013). Dynamical systems and models of continuous time. In T. D. Little (Ed.) The Oxford Handbook of Quantitative Methods, Vol. II, pp. 411-431. New York, NY: Oxford University Press.