This article proposes a new method for estimating derivatives on calculating the Empirical Bayes estimates of derivatives from a mixed model. Two simulations compare four derivative estimation methods: Generalized Local Linear Approximation, Generalized Orthogonal Derivative Estimates, Functional Data Analysis, and the proposed Empirical Bayes Derivative Estimates.
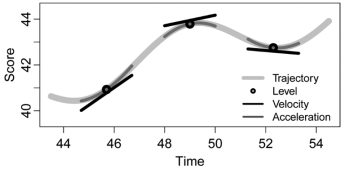
A wide variety of models can be understood in terms of the level, velocity, and acceleration of constructs: the zeroth, first, and second derivatives, respectively. Conceptualizing change in terms of derivatives allows precise translation of theory into method and highlights commonly overlooked models of change. We introduce the language of derivatives.
Many applied statistical problems address how change two variables are related. In this chapter derivatives are presented as a language framework for describing changes with respect to time. Derivatives can be used to provide statisticians and substantive researchers a common language that can be used to create better matches between models and theory.
The fitting of dynamical systems can be improved by estimating derivatives in a manner similar to that used to fit orthogonal polynomials. Two applications using simulated data compare the proposed method and a generalized form of Local Linear Approximation when used to estimate derivatives and when used to estimate differential equation model parameters.
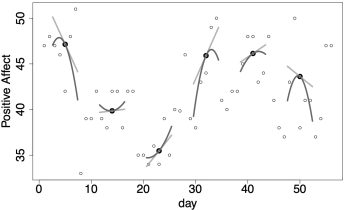
Intraindividual measures, such as intraindividual standard deviation or coefficient of variation, are incomplete representations variability. Studying variability can be made more productive by examining specific time scales. Furthermore, examination of variance in observed scores may not be sufficient. A method is introduced that uses estimated derivatives to examine variability at multiple time scales.
Brief summary of post contents Generalized Local Linear Approximation is a generalization of local linear approximation of derivatives (LLA, Boker & Graham, 1998). While LLA allows for estimation up to second-order derivatives (acceleration) with three observations, GLLA allows for any order of derivative with additional flexibility as to the number of observations used.
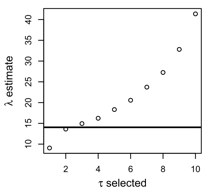
Methods for fitting the damped linear oscillator model using differential equation modeling can yield biased parameter estimates when applied to univariate time series. The bias depends on a researcher-selected, smoothing-like parameter. This article explores a technique that uses surrogate data analysis to select such a parameter, thereby producing approximately unbiased parameter estimates.