Many applied statistical problems address how change two variables are related. In this chapter derivatives are presented as a language framework for describing changes with respect to time. Derivatives can be used to provide statisticians and substantive researchers a common language that can be used to create better matches between models and theory.
Abstract
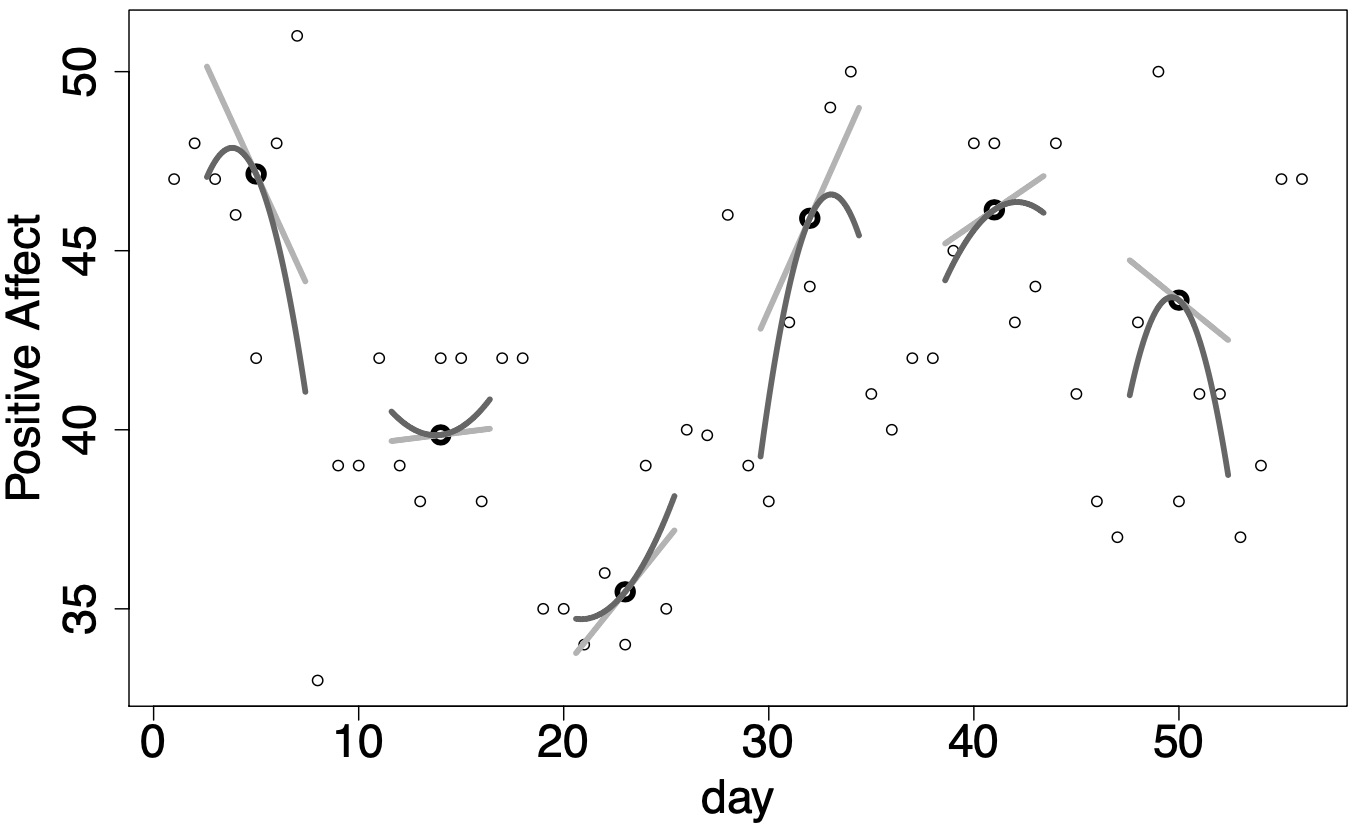
Many applied statistical problems address how the change in one variable is related to change in another variable. While the change of one variable with respect to another is the very definition of a derivative, the language of derivatives is not commonplace among social scientists. In this chapter we present derivatives as a language framework that is ideal for describing changes in variables, particularly changes with respect to time. This language can be used to understand many common models as relationships between derivatives rather than as disparate entities. Derivatives also can be used to provide statisticians and substantive researchers a common language that can be used to create better matches between models and theory. Moreover, this chapter will present derivatives as a language that has the potential to change the kinds of questions asked from variables measured repeatedly over time. Three differential equation models will be introduced for addressing questions related to the short–term fluctuation often described as intraindividual variability.
Citation
Deboeck, P. R., Nicholson, J. S., Bergeman, C. S., & Preacher, K. J. (2013). From Modeling Long-Term Growth to Short-Term Fluctuations: Differential Equation Modeling Is the Language of Change. In Millsap, R.E., van der Ark, L.A., Bolt, D.M., \& Woods, C.M. (Eds.), New Developments in Quantitative Psychology, pp. 427–447. New York: Springer.