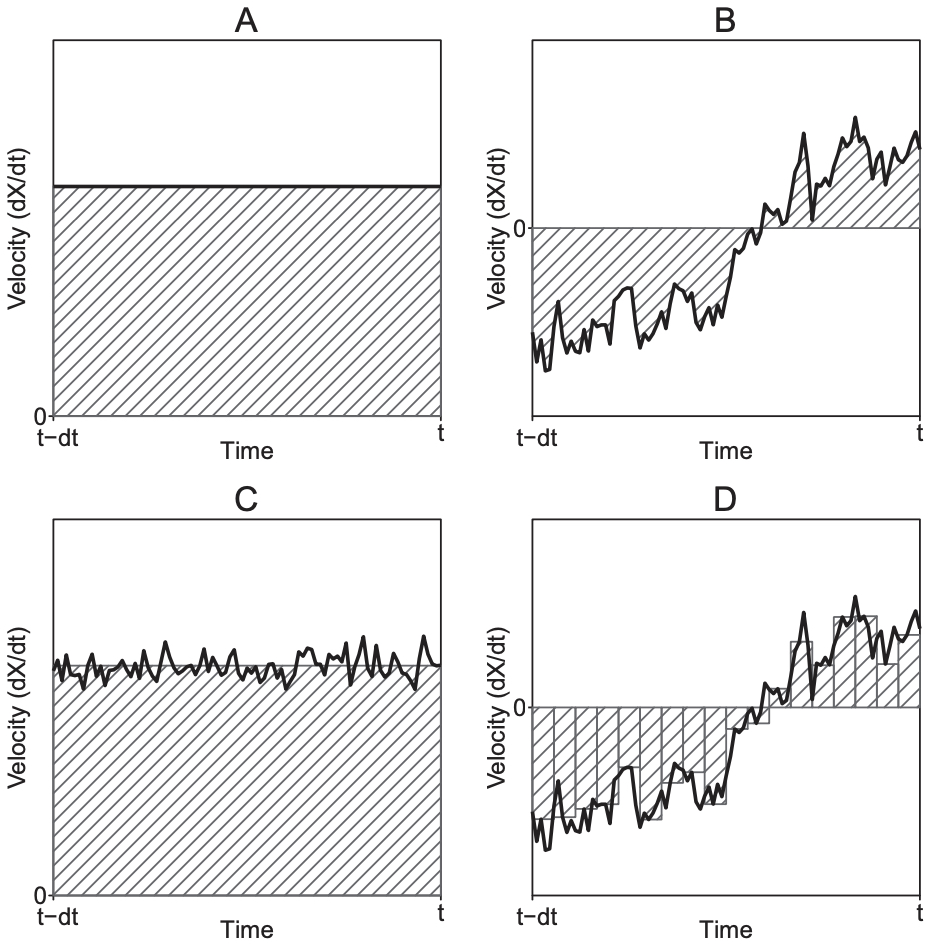
Stochastic differential equation (SDE) models are a promising method for modeling intraindividual change and variability. This method uses structural equation modeling (SEM) conventions to simplify SDE specification, the flexibility of SEM to expand the range of SDEs that can be fit, and SEM diagram conventions to facilitate the teaching of SDE concepts.
Abstract
Stochastic differential equation (SDE) models are a promising method for modeling intraindividual change and variability. Applications of SDEs in the social sciences are relatively limited, as these models present conceptual and programming challenges. This article presents a novel method for conceptualizing SDEs. This method uses structural equation modeling (SEM) conventions to simplify SDE specification, the flexibility of SEM to expand the range of SDEs that can be fit, and SEM diagram conventions to facilitate the teaching of SDE concepts. This method is a variation of latent difference scores (McArdle, 2009; McArdle & Hamagami, 2001) and the oversampling approach (Singer, 2012), and approximates the advantages of analytic methods such as the exact discrete model (Oud & Jansen, 2000) while retaining the modeling flexibility of methods such as latent differential equation modeling (Boker, Neale, & Rausch, 2004). A simulation and empirical example are presented to illustrate that this method can be implemented on current computing hardware, produces good approximations of analytic solutions, and can flexibly accommodate novel models.
Code and Other Content
Code here
Citation
Deboeck, P. R. & Boulton, A. J. (2016). Integration of Stochastic Differential Equations using Structural Equation Modeling: A Method to Facilitate Model Fitting and Pedagogy. Structural Equation Modeling, 23, 888–903.