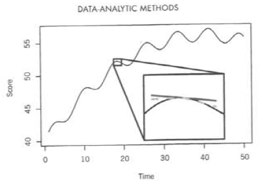
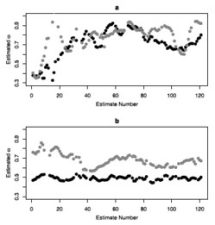
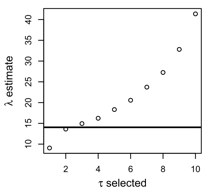
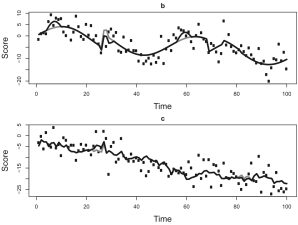
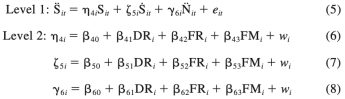Effective interventions may not be limited to changing means, but instead may also include changes to how variables affect each other over time. Continuous time models offer the opportunity to specify differing underlying processes. A substantive example compares models that imply different underlying continuous time processes using panel data.
Author: Pascal
Empirical Bayes Derivative Estimates (2020)
This article proposes a new method for estimating derivatives on calculating the Empirical Bayes estimates of derivatives from a mixed model. Two simulations compare four derivative estimation methods: Generalized Local Linear Approximation, Generalized Orthogonal Derivative Estimates, Functional Data Analysis, and the proposed Empirical Bayes Derivative Estimates.
Differing Perspectives on Time Alter Mediation Inferences (2018)
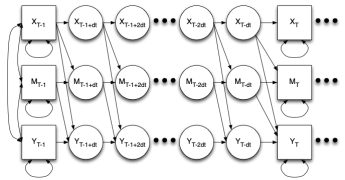
Time is unlike any other variable. This chapter considers the difference in perspectives offered by discrete-time and continuous-time approached to mediation. The differences in how one conceptualizes time have the potential to alter core mediation concepts as direct and indirect effect, complete and partial mediation, and even what constitutes a “mediation” model.
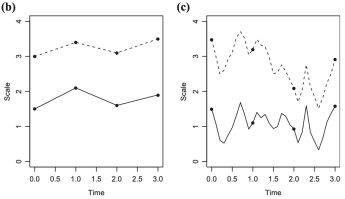
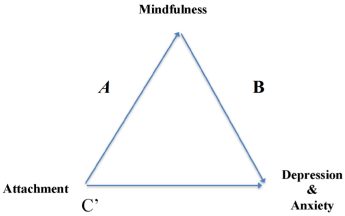
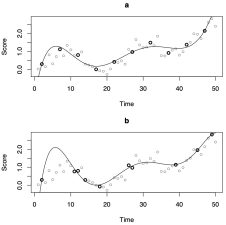
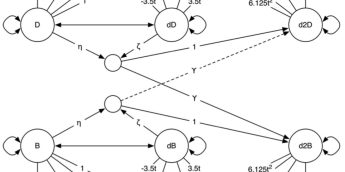
Attachment Changes predicting Depression and Anxiety Changes (2017)
Two studies examined the role short-term changes in adult attachment and mindfulness play in depression and general anxiety.
Dynamical Systems Approaches (2016)
This is an introduction to dynamical systems ideas. Dynamical systems are mathematical models of one or more constructs that change over time. Approaches to dynamical systems are concerned with describing the temporal evolution of constructs, with emphasis often placed on constructs that develop in a complex, nonlinear manner over time.
Integration of Stochastic Differential Equations (2016)
Stochastic differential equation (SDE) models are a promising method for modeling intraindividual change and variability. This method uses structural equation modeling (SEM) conventions to simplify SDE specification, the flexibility of SEM to expand the range of SDEs that can be fit, and SEM diagram conventions to facilitate the teaching of SDE concepts.
The Modeling of Change and Variability in Nursing Research (2015)
Most methods in statistics are focused on the analysis of mean differences. Mean–difference questions, however, represent only a narrow range of the questions that can be posed. Focusing only on these questions can overlook important questions concerning change and variability. This chapter considers methods to model change and variability.
Longitudinal Data Analysis (2015)
This essay reviews emerging trends in modeling repeated measures data. Three longitudinal models are discussed: panel model designs, growth curve models, and intensive within-person assessments. Continuous time models for panel data are discussed. The analysis of intensive within-individual observations is also considered, including work that limits the generalizability of interindividual studies to individual outcomes.
No Need to be Discrete: Continuous Time Mediation (2015)
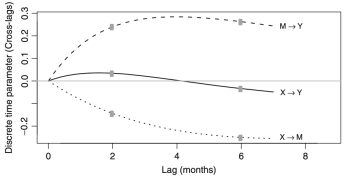
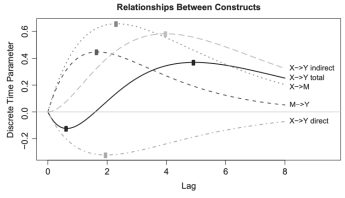
Mediation models based on cross-sectional data can produce unexpected estimates, so much so that making longitudinal or causal inferences is inadvisable. Even longitudinal mediation models produce estimates are specific to the lag between observations, leading to debate over lag selection. Using continuous time models, one can estimate lag-independent parameters.
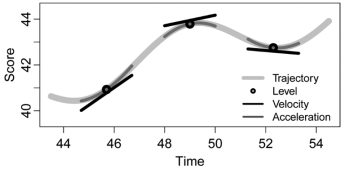
Using Derivatives to Articulate Change Theories (2015)
A wide variety of models can be understood in terms of the level, velocity, and acceleration of constructs: the zeroth, first, and second derivatives, respectively. Conceptualizing change in terms of derivatives allows precise translation of theory into method and highlights commonly overlooked models of change. We introduce the language of derivatives.
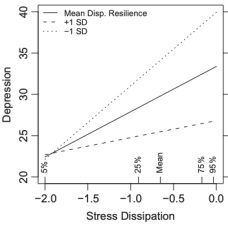
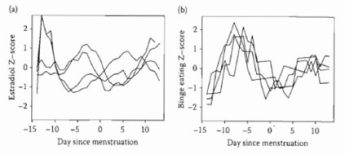
Stress dissipation effects on health and well-being (2014)
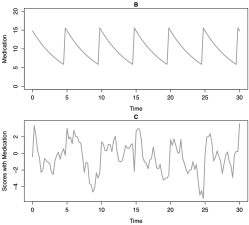
Daily data from the NDHWB (n = 783; age range 37–90) were analyzed to produce ‘dynamic characteristic’ estimates of stress input and dissipation. These were used in multi-level modeling (with age and trait stress resistance) to predict depression and health trajectories.
Differential Equation Modeling Is the Language of Change (2013)
Many applied statistical problems address how change two variables are related. In this chapter derivatives are presented as a language framework for describing changes with respect to time. Derivatives can be used to provide statisticians and substantive researchers a common language that can be used to create better matches between models and theory.
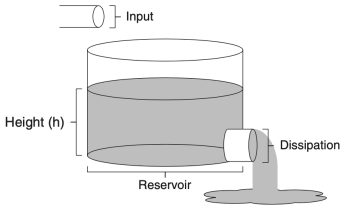
The Reservoir Model of Psychological Capacity (2013)
This article describes a model based on a reservoir. This model might be useful for constructs (e.g., stress), where events might “add up” (e.g., life stressors), but individuals simultaneously take action to “blow off steam” (e.g., engage coping resources). The model is applied to daily self-reports of negative affect and stress from older adults.
Dynamical systems and models of continuous time (2013)
Historically, it has been easier to describe differences between groups of people, rather than describe the dynamic ways that people change. This chapter introduces dynamical systems and of continuous time models. Two methods are introduced for the fitting of continuous time models to observed data: the approximate discrete model and latent differential equations.
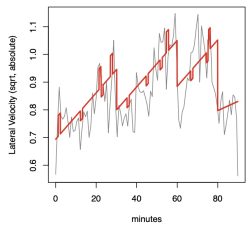
Gauging Driver Performance (2011)
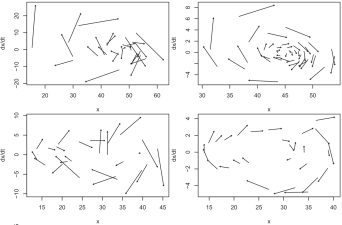
This paper examines the estimation of derivatives from in-vehicle measures of vehicle control such as steering wheel angle. At very short time scales many in-vehicle measures may indicate characteristics such as fatigue and inattention. This paper models changes in momentary derivative estimates in a 90-minute simulation with 19 participants.
Maternal Depressive Symptomatology and Child Behavior (2011)
This study investigated reciprocal relationships between adolescent mothers and their children’s well-being through an analysis of the coupling relationship of mothers’ depressive symptomatology and children’s internalizing and externalizing behaviors. The present study used dynamical systems to model time continuously, which allowed for the study of dynamic, transactional effects between members of each dyad.
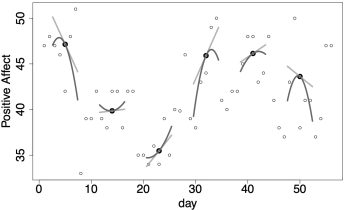
Perceived Emotion Control During Later Life (2011)
The relationship between global emotion control beliefs and daily affect reports across 56 days were assessed in a sample of 298 older adults. Variability analyses investigating multiple time scales revealed global beliefs were related to lower variance in negative affect and less variable speeds of negative affect change across a range of time scales.
Modeling Non-Linear Dynamics (2011)
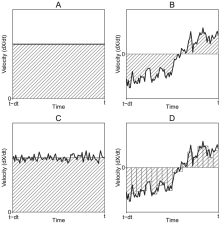
This chapter introduces one approach to describing constructs that consist of easily reversed, short–term changes — data that is often dismissed as “error.” This chapter begins with calculating rates of change on many small segments of a time series, and how the current state of a variable can be related to how it is changing.
Resilience-As-Process: Negative Affect & Stress (2010)
Resilience is often considered both a trait and a process. The current study proposes a new way to conceptualize resilience-as-process based on dynamical systems modeling, which allows researchers to capture the process of stress management in real time using coupled damped linear oscillator models.
Modeling Noisy Data with Observed and Expected Matrices (2010)
Using embedded and observed data matrices, a statistical approach to differential equation modeling is presented. This approach appears robust to short, poorly sampled time series with large proportions of measurement and dynamic error, as is common in psychological research.
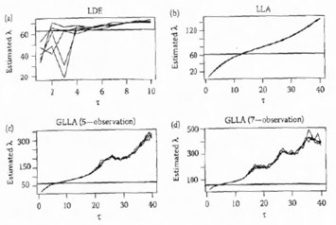
Generalized Orthogonal Derivative Estimates (GOLD) (2010)
The fitting of dynamical systems can be improved by estimating derivatives in a manner similar to that used to fit orthogonal polynomials. Two applications using simulated data compare the proposed method and a generalized form of Local Linear Approximation when used to estimate derivatives and when used to estimate differential equation model parameters.
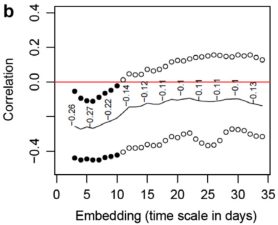
Derivative Variability Analysis (DVA) (2009)
Intraindividual measures, such as intraindividual standard deviation or coefficient of variation, are incomplete representations variability. Studying variability can be made more productive by examining specific time scales. Furthermore, examination of variance in observed scores may not be sufficient. A method is introduced that uses estimated derivatives to examine variability at multiple time scales.
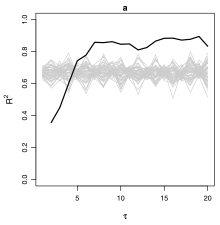
Smoothing–Independent Estimation of Oscillators (2009)
This article considers the estimation of damped linear oscillators with psychological data. The formulas of the new method presented in this chapter, which related the τ-conditional and τ-corrected estimates of model parameters, are described.
Generalized Local Linear Approximation (GLLA) (2009)
Brief summary of post contents Generalized Local Linear Approximation is a generalization of local linear approximation of derivatives (LLA, Boker & Graham, 1998). While LLA allows for estimation up to second-order derivatives (acceleration) with three observations, GLLA allows for any order of derivative with additional flexibility as to the number of observations used.
Modeling Oscillators Using Surrogate Data Analysis (2008)
Methods for fitting the damped linear oscillator model using differential equation modeling can yield biased parameter estimates when applied to univariate time series. The bias depends on a researcher-selected, smoothing-like parameter. This article explores a technique that uses surrogate data analysis to select such a parameter, thereby producing approximately unbiased parameter estimates.
Mood Oscillations Weather and RCBD (2008)
Rapid Cycling Bipolar Disorder outpatients completed twice-daily mood self-ratings for 3 consecutive months. These ratings were matched with local measurements of atmospheric pressure, cloud cover, and temperature. Several alternative second order differential equation models were fit to the data in which mood oscillations in RCBD were allowed to be linearly coupled with daily weather patterns.